尾崎塾
富田教室

[2018年1月10日]

必殺技は教えない

今日は中３生が苦戦する図形の問題を質問に来てくれました。


こんな問題です。

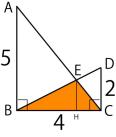
平行な長さ５と２の線の間にあるオレンジ色の三角形BCEの面積を求めなさいっていう問題です。

三角形の底辺４がわかっているので，高さEHがわかれば楽勝！

ですが，この高さを求めるのは難しいのです。

それで，この高さを求めようかと生徒に言うと，

「ななぶんのじゅう・・・ですか？」

と暗算してしまったのです。

ひょっとして天才少女？

どうしてわかったのか聞くと，必殺技を知っていたらしく，

「たしたぶんのかけたもの・・・」

たした５+２　ぶんの　かけた５×２

ということらしいです。


で，それは置いといて，相似な三角形を見つけてみると，



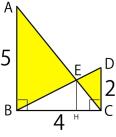
黄色どうしは相似だね。

で，赤の三角形に緑の三角形がハマっているでしょ。

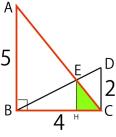
これも相似。

これらの相似比から高さEHを計算してやってみてちょ。

ということであとは自分でやらせました。


めんどうな計算をするとその必殺技と同じ答になるのです。

で，その必殺技は誰に教わったか聞くと，

なんと！

「学校の先生です！」

とのこと。


学校の先生って，相似の見つけ方やその式の立て方という本質的なところをちゃんと押さえておくのが仕事だと思うんです。

必殺公式を使って答だけ出せるようにするのは安モンの塾の仕事でっせ。


そういうわけで，ウチの塾は安モンの塾のように必殺技を教えてもらえないのです。

いちいち図を描いて考える。
そういうめんどくさい演習をする先にどんな応用でも効く実力がつくのだと考えています。

安易に必殺技に飛びつくと結局は自分のクビを絞めることになりますよ。←生徒もですが先生もね。



にほんブログ村



にほんブログ村